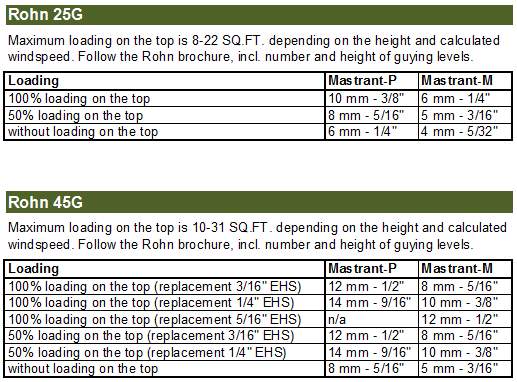
Rady a doporučení
Užitečné rady a doporučení
V tomto zajímavém videu kanálu "Practical Engineering" najdete řadu velmi užitečných informací a úvah, týkajících se kotvení stožárů (a vlastních antén). Je tam zamyšlení o samonosných stožárech, na jakém principu vlastně kotvení funguje, jaký účel má pata stožáru a hlavně proč je důležité většinu stožárů kotvit ve dvou či více úrovních.

Tento obecný návod vám ukáže, jak efektivně nastavit požadovanou délku kotevního lana, napnout ho a zajistit pro dlouhodobou instalaci.
Postup je vhodný jak pro instalaci jednoduchých stožárů, tak pro velké anténní systémy s příhradovými stožáry.
- Odšroubujte napínák na maximální délku.
- Nainstalujte napínací kroužek ke kotvě.
- Provlékněte lano horním okem/očnicí.
- Nainstalujte napínák smyčky na jeho volný konec. Použijte CL234 pro lana 6 až 11 mm nebo CL223 pro lana 3 až 6 mm.
- Nastavte požadovanou délku kotevního lana nebo jeho délku postupně upravujte. Je vhodné použít napínák a jeho snadné nasunutí na lano. Postup se bude lišit v závislosti na způsobu instalace stožáru/věže a kotevních lan (zvedání složeného stožáru ze země, postupné vysouvání teleskopického stožáru, instalace stožáru po částech, ...)..
- V pracovní poloze (před konečným napnutím) by napínací část měla vypadat takto:


- Po dokončení nastavení napněte lano pomocí napínáku.
- Nasaďte objímku a pevně ji utáhněte:


- Nyní můžete uvolnit napínák a uvázat alespoň 2 bezpečnostní uzly (dvojitý poloviční uzel):

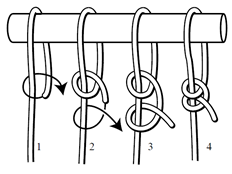
- Pevně utáhněte uzly a zajistěte volný konec lana kabelovou páskou (pro lana do cca 5 mm - 3/16") nebo nainstalujte druhou zajišťovací svorku.
- Napněte lano pomocí napínáku na požadované napětí:


- Pevně utáhněte svorky lana. Pokud používáte napínáky s pojistnými maticemi (jako tyto napínáky s vidlicemi na obr.), utáhněte je též.
- Než začnete, pročtětě si, prosím, tyto články Stručné zásady kotvení syntetickými lany a Doporučený postup instalace.

Navrhovaná náhrada ocelových lan syntetickými lany Mastrant - a to pouze na základě pevnosti!
| Ocel (1570 Mpa) | P | M |
| 4 mm | 6 | 4 |
| 5 mm | 8 | 5 |
| 6 mm | 10 | 6 |
| 7 mm | 12 | 8 |
| 8 mm | 14 | 10 |
| 9 mm | - | 12 |
| 10 mm | - | 12 |
| Pozinkovaný systém EHS | P | M |
| 5 mm 1x7 | 10 | 6 |
| 6 mm 1x7 | 14 | 8/10 |
| 8 mm 1x7 | - | 12 |

Při návrhu „kotevní soustavy“ (kotvícího lana s koncovkami, spojovacími prvky a úchyty) je nezbytné vzít v úvahu řadu faktorů:
- Pevnost soustavy je dána pevností nejslabšího článku. Proto je například zbytečné použít lano s pevností 50 kN spolu s napínákem o pevnosti 5 kN.
- I to nejdokonalejší syntetické lano je elastické – při jeho napínání se prodlužuje. V návrhu stožáru a jeho kotvení (stejně tak i při vyvazování antény) je třeba s touto vlastností počítat a vždy posoudit, jaký bude mít vliv na konstrukci prodloužení délky kotvicí soustavy. Pro určité situace bude muset být použito pevnější lano (s nižší absolutní roztažností), než by bylo třeba pro jinou konstrukci, které prodlužování délky kotev nevadí. Problém nastává především tam, kde je kotevní bod (Ground anchor point) příliš blízko patě stožáru (Tower base), nebo kdy jde o pevně zakotvený příhradový stožár (Lattice tower) s malou pružností. Vždy je vhodné provést kontrolní výpočet, o kolik se kotvicí soustava při zvoleném maximálním zatížení prodlouží a následně posoudit, jaký bude mít toto prodloužení vliv na její konstrukci či stabilitu.
- Lano je nutné ochránit před jakýmikoli ostrými hranami. Z tohoto důvodu je nutné lano zakončit očnicí (Thimble) či uvázat ke spojovacímu prvku (Coupler) s velmi hladkým povrchem. Zde je třeba si uvědomit, že nevhodné kovové materiály korodují, čímž dochází k zdrsňování jejich povrchu. Nikdy nevážeme lano přímo k betonovým sloupům či kamenům! Pokud chceme využít jako zemní kotevní bod třeba kámen, skálu či betonový sloupek, doporučujeme použít smyčku z ocelového lanka, ke které připojíme kotvicí lano pomocí hladkého spojovacího prvku.
- Velmi nebezpečné je pro lano tření o jakýkoli předmět v jeho trase, (např. větve, kameny, části staveb...). I napnuté lano se ve větru pohybuje a tento pohyb může způsobit prodření lana. Zvláště záludné (a tedy nebezpečné) je tření o větve stromů. Ty se vlivem větru pohybují často velmi intenzivně, a pokud se lano tře o větev, téměř jistě dojde k jeho poškození již během několika dní. Pokud používáte pro upevnění antén stromy, doporučujeme v místě ohybu přes větve použít ocelové lanko a syntetické lano napínat pomocí kladky.
- Spodní část kotvicí soustavy by měl tvořit ocelový úvazek délky 2-4 m (Steel rope cord). Ten zajistí, že syntetické lano nepřekousne nějaké zvíře nebo nedojde k jeho poškození lidskou činností (neúmyslnou či úmyslnou).
Zcela klíčovým prvkem pro bezpečnost je zakončení lana.
- Kotvicí lano je možné zakončit očnicí se svorkou (permanentní instalace), nebo jej přivázat k hladkému předmětu.

- Pro upevnění lana přivázáním doporučujeme, aby se lano vůči předmětu, ke kterému je přivázáno, nepohybovalo (třebaže jde o hladký upevňovací bod). To lze zajistit tím, že lano přivážeme ke spojovacímu prvku – rychlospojce (Chain quick-acting coupler), karabině (Spring hook) nebo třmenu (Shackle) - a ten teprve připevníme k upevňovacímu bodu.

- Za očnicí musí vždy následovat svorka. Doporučujeme duplexní svorky (Duplex clip) nebo svorky SIKA (Fist-grip). Za hlavní svorkou (tou, která je těsně za očnicí) je nutné volný konec lana zajistit bezpečnostním prvkem – druhou svorkou nebo několika smyčkami, podobně jako u tzv. „kotevního úvazu“ (Anchor hitch). Konec volného lana se dále pevně zabezpečí proti rozvázání například stahovacím páskem na kabely (Cable tie).


- Další možností je použít lisované svorky. Ty však je praktické použít pouze na jednom konci lana, jinak by nebylo možné upravovat jeho délku. Prodáváme je jako "lano s koncovkami" nebo "lano s očnicí" - zde.

- Při napínání dochází k zmenšování průměru lana a tím k jeho uvolňování ze svorky. Z toho důvodu je nutné svorky dotahovat při napnutém laně, tedy „pod zatížením“.
- Pozor na klasické „blajchrtky“ (Bull-dog grip)! Tyto lanové svorky, konstruované pro ocelová lana, mohou při vysokém stupni utažení syntetické lano „přestříhnout“. V žádném případě je proto nedoporučujeme jako hlavní svorky lanového zakončení – je možné je použít jako „bezpečnostní“ svorku za svorkou hlavní.
- Doporučujeme ke zvážení tzv. klínové svorky. Tyto svorky jsou sice poměrně drahé, ale oproti jiným mají několik výjimečných vlastností – jsou k lanu nejšetrnější, díky své „samosvornosti“ se napínáním utahují a umožňují pohodlnou změnu délky kotvící soustavy.

Nejčastější chyby a příčiny nehod:
- Kotevní bod je příliš blízko patě stožáru a tedy úhel svírající kotvicí lano a stožár je mnohem menší než 45°.
- Svorky nejsou utažené při napnutém laně.
- Za svorkami není bezpečnostní prvek (druhá svorka, uzel).
- Lano není zakončeno očnicí, ale je nevhodně přivázáno.
- Lano překouše zvíře nebo jej přeřízne vandal.
- V následujícím případě bylo použito lano s velkou roztažností.


- Spočítáme nebo změříme potřebnou délku kotvy ("kotevní soustavy").
- Přičteme délku potřebnou pro vytvoření zakončení. Pro standardní zakončení (očnice, svorka, uzel) je to cca 60-násobek průměru lana na každou stranu.
- Lano „uřízneme“ pomocí horkého předmětu s vhodnou hranou (např. hrotem pájky). Teplota tání polyesteru je cca 260°C, vláken Dyneema 150°C.
- Připravíme si vhodnou očnici. V případě potřeby můžeme očnici roztáhnout kleštěmi, navléknout na předmět, ke kterému bude kotva připevněna, a opět vrátit do původního tvaru. Malé deformace tvaru očnice nemají vliv na výslednou pevnost.
- Připravíme si vhodnou svorku, kterou před instalací rozebereme.
- Lano upevníme kolem očnice, umístíme do svorky a svorku smontujeme (viz obrázek). Volný konec lana ponecháme za svorkou dlouhý cca 35-násobek jeho průměru (pro vytvoření bezpečnostního uzlu).

- Svorku umístíme těsně k očnici – napínáním mezi svorkou a spojenými konci lana.
- Svorku pevně dotáhneme a vytvoříme uzel (viz obrázek). Volný konec lana pevně zajistíme stahovacím páskem na kabely proti rozmotávání.

- Svorky je nutné dotahovat opakovaně, při postupném napínání lana. Konec kotvy, který nebude po jejím napnutí přístupný, je tedy nutné dotáhnout před vlastní instalací. Očnici upevníme k pevnému bodu a lano postupně v několika krocích napínáme. Po každém zvětšení napínací síly dotáhneme šrouby na svorce. Ideální je, když poslední dotažení provádíme při dosažení maximálního pracovního zatížení (30 % pevnosti). U silnějších lan je však tento ideál obtížně dosažitelný – napínání provádíme například tak, že lano napnuté mezi dva pevné body zatěžujeme kolmo k jejich ose, můžeme si pomoci například automobilem či provizorně vytvořeným kladkostrojem.
- Kotvu upevníme na místo, kde bude používána. Postupně jí napneme a dotáhneme svorky (viz předchozí bod).
- Vizuálně zkontrolujeme, zda nedošlo k proklouznutí lana ve svorce – pokud ano, znamená to, že jsme nezvolili vhodný postup napínání a utahování, případně že je svorka vadná.
- Pro napínání lana můžeme použít závitové napínáky. U teleskopických stožárů se můžeme obejít bez napínáků – stožár (příslušný díl) trochu snížíme, utáhneme svorky a poté jej vrátíme do stabilní polohy – vhodnost tohoto postupu je samozřejmě pro každý typ stožáru různá.
- Optimální klidové napnutí lana je závislá na řadě faktorů - konstrukci a pevnosti stožáru, typu a síle lana, vzdálenosti paty stožáru od kotevního bodu. Ve většině aplikací nejlépe vyhovuje síla 5-20% pevnosti lana.
- Po finálním napnutí kotev do „klidového stavu“ se bude lano ještě nějakou dobu „usazovat“. Kotvy zkontrolujeme a v případě potřeby dopneme následující den po instalaci a následně zhruba 3x vždy s odstupem cca 1 týdne. Vždy musíme dodržet správný postup dotahování svorek!
Nejčastější chyby a příčiny nehod:
- Kotevní bod je příliš blízko patě stožáru a tedy úhel svírající kotvicí lano a stožár je mnohem menší, než 45°.
- Svorky nejsou utažené při napnutém laně.
- Za svorkami není bezpečnostní prvek (druhá svorka, uzel).
- Lano není zakončeno očnicí, ale je nevhodně přivázáno.
- Lano překouše zvíře nebo jej přeřízne vandal.
Martin Huml, OL5Y/OK1FUA,
Při svých radioamatérských aktivitách se asi jako každý z nás z velké části věnuji otázce antén. A jedním z nejdůležitějších a možná nejnáročnějším úkolem je anténu dostat „do vzduchu" a tam jí i udržet. Platí to zřejmě pro všechny antény, s výjimkou snad pouze antén beverage... Tomuto tématu jsem se věnoval v článku „Jak stavět a kotvit jednoduché stožáry" (Radioamatér 2 a 3/2004). Již ale tenkrát při jeho psaní jsem cítil, že tato problematika je natolik zajímavá, komplexní a rozsáhlá, že bude vhodné se k ní vrátit.
Motivem k napsání následujícího pojednání byly rovněž otázky, které mi položil ať již někdo ze známých, či se v mé hlavě objevily samy, např. „proč kotvíš ten vertikál tak nízko?", „bude tenhle provaz stačit?", „unese ten stožár tu anténu?" a podobně. A dost často jsem nenašel jinou odpověď, než „protože si myslím, že to stačí" nebo „protože jsem to tak někde viděl". To nezní příliš důvěryhodně. Praxe a zkušenosti jsou sice skvělé a nenahraditelné, ale všeho moc škodí. A tak, když mě i pracovní aktivity přivedly k otázce „kotvení", rozhodl jsem se, že se na to podívám i teoreticky. Hned v úvodu chci uvést, že nejsem strojař, a proto jsem se po delší době hledání „dal dohromady" s panem Ing. Richardem Beberem, který na rozdíl ode mne danou problematiku vystudoval. Tímto mu chci velmi poděkovat - nebýt ho, tento článek by zřejmě nevzniknul.
Jak už vyplývá z názvu článku, naším tématem jsou antény kotvené. To však neznamená, že majitelé nekotvených stožárů zde nenajdou nic zajímavého. Užitečné mohou být například výpočty sil působících na antény ve větru či jiné souvislosti.
Používané pojmy a zjednodušení
Prosím odborníky a jazykovědce o shovívavost - používám termíny tak jak je znám z převážně amatérské praxe:
● místo (bod) upevnění = tam kde je kotvící lano připevněno ke stožáru
● výška upevnění = vzdálenost bodu upevnění od paty stožáru
● místo (bod) ukotvení = tam kde je kotvící lano připevněno k zemi (či jinému pevnému bodu)
● vzdálenost ukotvení = vzdálenost kotvícího bodu od paty stožáru
● sestava = stožár s anténou
Vertikální anténa je vlastně stožár bez antény. Proto v dalším textu nebudu mezi těmito dvěma typy antén rozlišovat, pokud to nebude účelné. Jinými slovy např. obrat „ukotvení v polovině stožáru" bude možné chápat jako „ukotvení v polovině vertikálu".
Pokud není uvedeno jinak, předpokládáme, že stožár je postaven na vodorovném povrchu, tedy kotvicí body a pata jsou v jedné rovině, kolmé k ose stožáru. Je to z důvodu názorné jednoduchosti - je jasné, že realita bývá jiná. Proto v dalším textu bude uvedeno, jak se s realitou vypořádat.
Při našich úvahách se rovněž nezabýváme chováním vlastní antény - předpokládáme, že anténa na stožáru se nemění.
No a nakonec něco pro ty, jež nejsou s fyzikou moc kamarádi - budeme hodně mluvit o síle, jejíž jednotkou je 1 N (Newton). Pro představu - pokud zvednete závaží o hmotnosti 1 kg, působí na vás silou přibližně 10 N.
Anténa a stožár
Pokud se podíváme na zjednodušený model kotveného stožáru a antény na jeho vrcholu (obr. 1), budou na tuto sestavu působit tyto síly:
● gravitační síly (hmotnost stožáru, lan a antény),
● odporová síla větru,
● předepínací síly kotvících lan.
Soubor těchto sil vyvolá reakci, tak aby výsledné síly byly v rovnováze. Reakce se projeví v uchycení paty stožáru a v místech upevnění kotvících lan. Rovněž dojde k pružným deformacím stožáru a lan. Neuvažujeme nevratné deformace či destrukci materiálu - právě těmto případům bychom chtěli předejít a proto se budeme věnovat stanovení všech působících sil.
Ale síly nejsou vše, co bude mít na chování sestavy vliv. Nesmíme zapomenout na konstrukci stožáru (trubka, příhradová konstrukce apod.) a materiál, ze kterého je vyroben, konkrétně jeho fyzikální vlastnosti, jako hustota (měrná hmotnost), pružnost a pevnost. Podobně potřebujeme znát vlastnosti použitých kotvicích lan - pevnost a tažnost. Zrekapitulujme si tedy, co musíme vědět:
● anténa - hmotnost
● anténa - tvar (počet, délky a průměry prvků)
● stožár - konstrukce, materiál
● kotvící lano - tažnost (prodloužení při známém zatížení), pevnost
No a vlastní parametry, se kterými budeme pracovat, jsou:
● celková výška (výška antény nad zemí = výška stožáru)
● počet kotvících směrů (3 nebo 4)
● počet kotvících pater (v kolika úrovních bude stožár kotven)
● výška upevnění
● vzdálenost ukotvení
Vzdálenost ukotvení
První otázkou, kterou se budeme zabývat, je, jaký vliv má na velikosti sil (působících na stožár a kotvící lana) vzdálenost ukotvení. Rozdělíme si úlohu na mezní situace - při první fouká vítr přímo ze směru ukotvení, při druhé fouká „mezi kotvami". (obr. 2)
Fouká-li vítr ze směru od kotvícího bodu, jde o triviální skládání sil - případ pravoúhlého trojúhelníku, kdy jednu odvěsnu tvoří stožár (h), druhou vzdálenost mezi patou stožáru a kotvícím bodem (r), přičemž kotvící lano je přepona (l). V poměru, ve kterém jsou jednotlivé strany tohoto trojúhelníka, jsou i síly působící jednotlivými směry. Známe (spočítáme) sílu Fant působící na anténu způsobenou větrem. (Její konkrétní hodnota není pro tuto chvíli důležitá, budeme se tím zabývat v dalším textu - jde nám nyní o posouzení vlivu vzdálenosti kotvícího bodu.) Tedy síla působící na stožár (v jeho ose) Fst = Fant * h / r, síla působící na kotvící lano Fko = Fant * l / r.
Délku lana l spočítáme Pythagorovou větou: l = √ (h2 + r2).
Při větru foukajícím ze směru osy mezi kotvami je situace nepatrně složitější, neboť musíme brát v úvahu úhel, jaký kotvy mezi sebou svírají - jinými slovy, do kolika směrů je stožár kotven.
Kotvící směry
Pro tento účel se podíváme na stožár seshora a představíme si celkem 3 body - stožár a 2 kotvící body. Dále si představíme směr, ze kterého fouká vítr - je to osa mezi kotvícími body procházející stožárem. Tam, kde tato osa protíná spojnici mezi oběma našimi kotvícími body je bod, který představuje virtuální kotvící bod pro výpočet působících sil. Vidíme, že je mnohem blíže patě stožáru, než vzdálenost ukotvení - tím blíže, čím větší je úhel mezi kotvami.
Jde opět o trojúhelníky, tentokrát již ne vždy pravoúhlé. Aplikujeme-li základní goniometrické funkce, dojdeme ke vztahům:
pro 4 kotvy po 90°:
Fst = Fant * (h / r) * √2 = Fst = Fant * (h / r) * 1,414
Fko = Fant * (l / r) * (√2) / 2 = Fant * (l / )r * 0,707
pro 3 kotvy po 120°:
Fst = Fant * (h / r) / cos(60/180π) = Fant * (h / r) / 0,5
Fko = Fant * (l / r) / cos(60/180π) = Fant * (l / )r .
Na první pohled možná není vidět jedna zajímavost - při kotvení do 3 směrů je síla působící na kotevní lano stejná jak při větru „od kotvy", tak „mezi kotvami".
Jak to vypadá v praxi
Od teorie, jež je pravděpodobně pro většinu z vás zbytečně nudná, přejděme k praktickým dopadům. (Slibuji, že další povídání již bude bez vzorečků - byly by totiž už mnohem složitější...)
Pro názornost jsem zvolil jednoduchý příklad - stožár o výšce 10 m s KV tribanderem ECO (10/15/20m) na jeho vrcholu. Znovu opakuji - jde o příklad pro ukázání dopadu vzdálenosti ukotvení a do kolika směrů je stožár kotven. Nezajímají nás tedy vlastnosti stožáru ani lan. Takže - na tribander necháme foukat vítr o rychlosti 130 km/h. Jak lze přibližně spočítat, takový vítr na něj působí silou přibližně 775 N. K tomu, jak jsem na to přišel, se vrátíme v následující kapitole, pro tuto chvíli nám tento výsledek postačí.
Zmíním nyní však jeden důležitý fakt, a to že síla je úměrná čtverci (druhé mocnině) rychlosti (tedy např. poloviční rychlost = čtvrtinová síla, pro 80 km/h bude naše síla cca 290 N). Podobně však i roste - člověk pak pochopí, co mohou napáchat různá tornáda s rychlostmi větru v centru přes 300 km/h a nemyslí si, že poletování aut je jen výmyslem amerických filmařů.
Ale zpět nyní ke kotvení. V následujících tabulkách vidíte spočítané síly pro obě verze kotvení (3 a 4 směry) a pro vzdálenost ukotvení 10 a 5 m. Je myslím zřejmé, že přibližování kotvicích bodů ke stožáru způsobí zbytečné zvyšování působících sil. Stejně tak kotvení do 3 směrů, jež zvyšuje zatěžování stožáru.
Jak vidíte, při rozumném uspořádání nejsou síly ani při tomto silném větru nijak obrovské. Jinými slovy - pro ukotvení takovéto antény nepotřebujeme žádná extrémní lana. Jak lze dohledat na mnoha místech, i poměrně slabé lanko, pokud je určené pro tento účel, svou pevností postačí. Nejslabšími místy totiž bývají všechny spoje... A v našich podmínkách nesmíme zapomínat ani na situace, kdy je anténa obalená námrazou... Ale to už jsem opravdu jinde, vrátíme se k tomu.
Jen pro úplnost ještě jeden odstavec - pozorným čtenářům jistě neušlo, že nejde o absolutní výšku a vzdálenost - naprosto stejné výsledky dostaneme při stožáru 20 m a vzdálenostech 20 a 10 m. Jde o úhel svíraný mezi kotvícím lanem a stožárem. To je třeba si uvědomit především v situaci, kdy kotvící bod nelze umístit do roviny kolmé na stožár (je ve svahu). Pokud byste například museli v uvedeném příkladě umístit kotvící bod o 3 m níže, než je pata stožáru, a chtěli byste zachovat úhel mezi lanem a stožárem 45°, musíte umístit kotvicí bod 13 m od osy stožáru (pozor, ne od jeho paty!). To se může někdy poměrně špatně odměřovat, proto je možné vypočítat a odměřit délku kotvícího lana - ta bude v tomto případě dlouhá 13 * 1,41 = 18,3 m (1,41 = √2).
Síla větru
Pokud do proudu tekutiny, v našem případě vzduchu, umístíme těleso, bude na něj působit odporem daným třecí a tlakovou složkou. Tento odpor se stanovuje experimentálně v aerodynamických tunelech a je vyjádřen vztahem pro odporovou sílu:
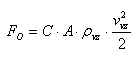
kde FO je odporová síla [N], C je součinitel odporu tělesa (-), A je plocha tělesa kolmá na směr větru [m2], ρvz je hustota vzduchu [kg/m3] a vvz je rychlost větru [m/s].
Hodnota odporového součinitele není konstantní, ale je závislá na tzv. Reynoldsově číslu - bezrozměrnému kritériu, vyjadřujícímu poměr sil setrvačných a viskózních:
Re = vvz * d /v
kde d je charakteristický rozměr [m] a v je kinematická viskozita vzduchu.
Pokud anténu (v našem případě zmíněný tribander) zjednodušíme na několik rotačních válců, pak je charakteristickým rozměrem jejich průměr a pro běžné podmínky je Re rovno řádově 104 a součinitel odporu tělesa C je přibližně 1,2. Odporovou sílu působící na anténu (trubka průměr d = 35 mm, délka l = 23,6 m, rychlost větru vvz = 36 m/s = 130 km/h; hustota vzduchu 1,2 kg/m3) můžeme tedy stanovit:
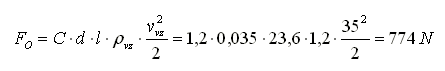
Tato síla působí jako spojité zatížení na celou anténu (pokud si reálnou situaci zjednodušíme na stejný rychlostní profil větru po celé ploše antény). Obdobným způsobem můžeme stanovit odporovou sílu působící na stožár.
V následující tabulce jsou pro ilustraci uvedeny spočítané síly pro několik typických antén (omlouvám se těm, kteří svou anténu v tabulce nenašli a přesto jí považují za „typickou").
Co udělá námraza
Námraza, která je v našich podmínkách velmi podstatným prvkem majícím vliv na fungování (i přežití) antény, způsobí
● zvětšení plochy na kterou působí vítr a
● zvýšení hmotnosti.
Protože já osobně nemám s námrazou prakticky žádné zkušenosti, konzultoval jsem tuto otázku s několika přáteli, kteří mají své antény na různých problematických místech, včetně takových, kde je námraza několikaměsíční záležitostí. Z jejich zkušenosti vyplývá, že námraza na prvcích tvoří obvykle 50-100 % původního průměru, v extrémních případech až 200 % (prvek tedy zvětší svůj průměr 3x). Jak je to tedy se zvětšením sil?
Z předchozí kapitoly vyplývá, že odporová síla větru je přímo úměrná ploše antény kolmé na směr větru a tedy vlastně průměru jejích prvků. Takže zvětší-li se průměr prvků 2x, zdvojnásobí se i síla větru. To jsou velmi jednoduché počty - chcete-li anténní sestavu dimenzovat na extrémní námrazu, vynásobíte síly 3x.
S hmotností je to složitější. Pro její výpočet potřebujeme, kromě tloušťky námrazy, znát její hustotu. Přestože hustota ledu je 917 kg/m3, hustota námrazy se v literatuře a normách uvažuje 400-500 kg/m3 - počítejme tedy raději 500 kg/m3. Protože nás zajímá, kolikrát se zvětší hmotnost již existující antény, potřebujeme rovněž znát hustotu materiálu, ze kterého je vyrobena. To bývá obvykle nějaká hliníková slitina, jejíž hustota je kolem 2800 kg/m3.
K vlastnímu výpočtu jen stručně. Pro zjednodušení opět uvažujeme, že anténa se skládá z trubek, případně z tyčí (VKV). Hmotnost tělesa m = V * ρ, kde V je objem a ρ hustota. Objem rotačního válce je V = π * r2 * l, kde r je poloměr a l délka. Dosadíme-li známé hodnoty, spočítáme původní hmotnost i hmotnost námrazy. Situaci ukazuje názorně následující přehled.
Tabulka ukazuje pro někoho možná šokující fakta. Není jednoduché si připustit, že anténa sestavená např. z trubek průměru převážně 24 mm se stěnou 1 mm zvýší při námraze 100 % svou hmotnost 4,4x! Na druhou stranu je třeba si uvědomit, že podmínky pro vytvoření souvislé námrazy po celém obvodě trubky, zvláště u trubek větších průměrů, bývají v běžných QTH poměrně vzácné.
Pro zajímavost: o námraze říká encyklopedie Wikipedia následující:
Námraza je atmosférický jev, který se projevuje vznikem ledových krystalů na povrchu objektů působením následující vlivů:
• mrznutím drobných kapének vzdušné vlhkosti (mraků, mlhy apod.) při jejich styku s povrchem země, objektů nebo jiných předmětů o teplotě 0°C a nižší;
• srážením (sublimací) vzdušné vlhkosti na dostatečně prochlazeném zemském povrchu nebo předmětech, a to i bez přítomnosti mlhy nebo oblačnosti.
Nejvyšší pravděpodobnost vzniku námrazy je při styku prochlazeného (0 až -4 °C) povrchu objektů s vlhkým vzdušným prouděním. Při teplotách pod -4 °C a nižších výrazně klesá možnost vzniku a při teplotách pod -12 °C námraza téměř nevzniká nebo je velice slabá.
Výše uvedené údaje jsou zajímavé především pro úvahy o konstrukci antény - do jaké míry budou prvky a ráhno dimenzovány a případně vyvazovány proti prohnutí. To je však již opět zcela jiné téma.
V příštím pokračování se již začneme zabývat kotvením reálného stožáru, včetně uvažování jeho pevnosti a dalších ovlivňujících prvků.
Martin Huml, OL5Y/OK1FUA,
V prvním díle jsme si něco řekli o silách a problematice kotvení obecně, dnes si začneme povídat o stožáru jako takovém. Ještě než začnu, chci poděkovat za všechny ohlasy, otázky a další náměty. Jsem rád, že vás článek zaujal a budu se snažit, aby tomu tak bylo i nadále.
V tomto pokračování se budeme věnovat nejzákladnější variantě - tedy trubkovému stožáru kotvenému v jedné úrovni pod anténou. Tato situace je znázorněna na obrázku 1. Pro zjednodušení výpočtů uvažujeme, že celý stožár je z trubky stejného průměru a stejných vlastností po celé délce. Rovněž budeme předpokládat, že rychlost větru je po celé délce stožáru stejná (ve skutečnosti bývá těsně nad zemí nižší).
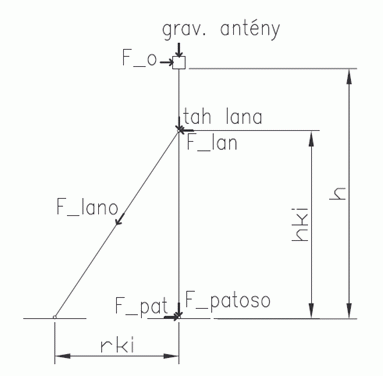
Při rozboru veličin a vlastností, které mají vliv na chování soustavy, dojdeme k tomuto výčtu:
- celková výška stožáru, výška uchycení lana, vzdálenost kotvy od paty stožáru (pro určení sil, jež na soustavu působí)
- vnější a vnitřní průměr trubky (pro určení pevnosti a hmotnosti stožáru)
- fyzikální vlastnosti materiálu, ze kterého je trubka vyrobena: hustota, modul pružnosti, mez pevnosti, mez úměrnosti (pro určení pevnosti a hmotnosti stožáru)
- plocha a hmotnost antény (pro určení odporové síly větru)
- součinitel odporu stožáru a antény (pro určení odporové síly větru)
- vlastnosti prostředí (vzduchu): kinetická viskozita, gravitační zrychlení, hustota vzduchu
- rychlost větru
Výstupy výpočtů, jež nás budou zajímat:
- síla v ose stožáru v patě (působení na bod umístění paty stožáru)
- síla v ose lana (pro volbu vhodného lana)
Zajímat nás však bude především bezpečnost - zda stožár vydrží a s jakou mírou bezpečnosti.
Jak však posuzovat a porovnávat bezpečnost, když nemá žádnou jednotku a i její vyjádření slovy je poměrně obtížné a především subjektivní? Ani změřit pravděpodobně nepůjde. V konstruktérských odvětvích se používá veličina označovaná jako koeficient bezpečnosti. Ten se pro každý druh konstrukce vypočítává odlišně, jeho interpretace (smysl) je však vždy stejný: Pokud je větší než 1, „je teoretická jistota, že konstrukce vydrží". Doporučená minimální hodnota je 1,4. Pokud se na bezpečnosti konstrukce podílí více faktorů, počítá se její koeficient pro každý faktor zvlášť a celkovou bezpečností soustavy je ten nejmenší z nich. V našem případě jsou kritické faktory 2: pevnost materiálu, ze kterého je stožár vyroben (tedy napětí v něm) a vzpěr stožáru (aby se stožár neprohnul). Výsledkem našich úvah bude tedy posouzení celkové bezpečnosti soustavy.
Z výše uvedeného je zřejmé, že veličin, které jsou pro konkrétní situace různé, je velké množství. Každý má jinou anténu, jiný stožár, jinou výšku stožáru... Pro názornost jsem tedy vybral několik situací, které mi připadají vhodně ukázkové a pro něž jsem spočítal jednotlivé výstupy. Pro každý případ jsem zvolil takovou výšku uchycení lana, aby celková bezpečnost vycházela co největší. Jednotlivé varianty jsou tyto:
- Stožár výšky 13 m, na němž je umístěná anténa ECO (3el. tribander pro 10/15/20m). Tato varianta je spočítána pro 3 různé stožáry: trubka průměru 80 mm se sílou stěny 3 mm z průměrně kvalitního duralu (var. A), trubka ze stejného materiálu 100/4 mm (B) a ocelová trubka 60/3 mm (C).
- Stožár výšky 13 m s 11el. anténou pro pásmo 2 m ve 2 variantách: průměrný dural průměru 60 mm se stěnou 2 mm (D) a laminát průměru 60 mm se stěnou 5 mm (E).
- Poslední variantou je stožár vysoký 23 m s mohutnou anténou TH7DX (7el. tribander pro 10/15/20m) opět ve 2 variantách: kvalitní dural průměru 100 mm se stěnou 10 mm (F) a ocel průměru 100 mm se stěnou 5 mm (G).
Ostatní parametry použité pro výpočty jsou: hustota vzduchu = 1,2 kg/m3, gravitační zrychlení = 9,82 m/s2, rychlost větru = 36 m/s = 130 km/h, součinitel odporu stožáru a antény C = 1,2. Výsledky jsou uvedeny v tab. 1.
| Veličina | Symbol | A | B | C | D | E | F | G | Jednotka | |
|
11m |
11m dural ECO |
11m ocel ECO |
11m dural 11el. 2m | 11m laminát 11el. 2m | 23m dural TH7DX |
23m ocel TH7DX |
||||
| stožár - trubka | ||||||||||
| výška celková | h | 13 | 13 | 13 | 13 | 13 | 23 | 23 | m | |
| výška uchycení lana | h_ki | 12 | 12 | 12 | 11 | 9 | 17 | 20 | m | |
| vzdálenost kotvy | r_ki | 10 | 10 | 10 | 10 | 10 | 15 | 15 | m | |
| vnější průměr | D_o | 80 | 100 | 60 | 60 | 60 | 100 | 100 | mm | |
| vnitřní průměr | D_i | 74 | 92 | 54 | 56 | 50 | 80 | 90 | mm | |
| hustota stožáru | ro_s | 2700 | 2700 | 7850 | 2800 | 1200 | 2800 | 7850 | kg/m3 | |
| modul pružnosti | E_s | 60000 | 60000 | 200000 | 60000 | 18000 | 60000 | 200000 | MPa | |
| mez pevnosti | sigma_t | 300 | 300 | 320 | 300 | 220 | 350 | 320 | MPa | |
| mez úměrnosti | sigma_tu | 200 | 200 | 120 | 200 | 200 | 200 | 120 | MPa | |
| reakce lana | F_ropex | 1355 | 1486 | 1223 | 629 | 768 | 2446 | 2079 | N | |
| reakce v patě v ose | F_patoso | 2023 | 2346 | 2153 | 856 | 858 | 4951 | 5808 | N | |
| reakce v paté kolmá | F_pat | -381 | -492 | -270 | -267 | -128 | -376 | -743 | N | |
| síla v ose lana | F_lano | 2116 | 2321 | 1911 | 934 | 1034 | 3697 | 3466 | N | |
| anténa | ||||||||||
| plocha antény | S_ant | 0,82 | 0,82 | 0,82 | 0,18 | 0,18 | 0,9 | 0,9 | m2 | |
| hmotnost antény | m_ant | 15 | 15 | 15 | 3,5 | 3,5 | 40 | 40 | kg | |
| posouzení bezpečnosti | ||||||||||
| napětí ve stožáru | k_n | 4,01 | 6,21 | 2,86 | 2,37 | 2,14 | 3,16 | 3,34 | ||
| vzpěr | k_v | 2,47 | 5,84 | 3,62 | 2,01 | 1,89 | 3,27 | 4,75 | ||
| celková bezpečnost | k | 2,47 | 5,84 | 2,86 | 2,01 | 1,89 | 3,16 | 3,34 | ||
Na variantě (A) bych chtěl ukázat skutečnost, že přestože je použita poměrně silná trubka, celková bezpečnost není nijak oslnivá, jak možná někteří na základě zkušeností čekali. Je to dáno tím, že uspořádání sestavy s jedinou kotvící výškou není rozhodně optimální a klade vysoké nároky na pevnost materiálu stožáru. O jiných variantách si povíme příště, již teď vám ale prozradím, že pevnost soustavy při dvojím kotvení je čtyřnásobná a dokonce devítinásobná při 3 kotvicích úrovních (samozřejmě pokud jsou umístěny v optimálních výškách). Variantu (E) jsem zařadil proto, neboť jsem podobné stožáry viděl použité u některých radioamatérů.
| materiál | hustota | modul pružnosti | mez pevnosti | mez úměrnosti |
| kg/m3 | MPa | MPa | MPa | |
| dural | 2800 | 60000 | 180-450 | x |
| hliník | 2700 | 60000 | 60-150 | x |
| ocel | 7850 | 200000 | 320-835 | 120-290 |
| laminát | 1200 | 18000 | 220 | x |
Tab. 2: fyzikální vlastnosti materiálů
Kromě vlastní bezpečnosti soustavy je zajímavé podívat se i na rozložení některých veličin po délce stožáru. To ukazují obrázky 2 (pro variantu C) a 3 (E). Pokud je výška kotvení volena ve výšce pro dosažení co nevětší bezpečnosti, jsou tvary křivek velmi podobné - proto uvádím pouze 2 typické příklady. Pro přesnost ještě doplňuji, že veličiny jsou počítány po jednotlivých metrech a výslednými body je poté proložena křivka grafu.
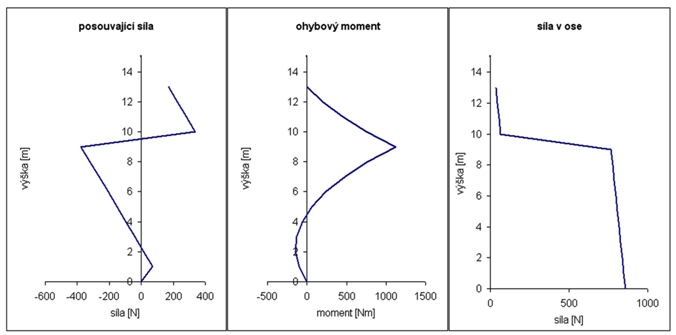
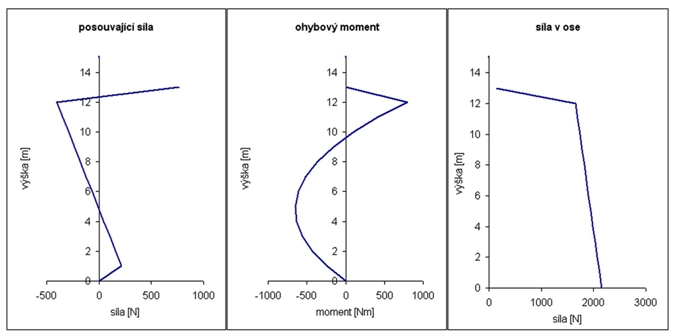
V příštím pokračování se budeme zabývat metodami, jak zvýšit pevnost (a tedy i bezpečnost) sestav, resp. jak optimalizovat konstrukci tak, aby byla sestava byla bezpečná a přitom co nejsnadněji realizovatelná.

Základ této jednoduché metody je snadný: uchopíte lano uprostřed dvou bodů a táhnete za něj do stran, abyste dosáhli určitého posunu. Změřte sílu potřebnou k dosažení tohoto posunu (například pomocí pružinové váhy). Čím větší je síla potřebná k dosažení stejného posunu, tím větší je napětí (což je zřejmé).
Napětí můžete také vypočítat:
- Vzdálenost mezi body na laně: L [mm]
- Posunutí: D [mm]
- Tažná síla: F [N]
- Tahová síla: T [N]
T = F * L / D / 4
Vzorec je poměrně přesný, pokud je vzdálenost mezi body mnohem větší než posunutí (L >> D).
Zde je jeden z mnoha přístrojů založených na tomto principu:

Na trhu je mnoho různých měřicích nástrojů, například tento od společnosti Loos&co. Buďte opatrní, protože tyto napínáky jsou kalibrovány pro ocelová lana, nikoliv pro syntetická. Měřidla pro ocelová lana mají obvykle malou vzdálenost mezi měřicími body.
Dobrým ukazatelem napětí v laně je jeho průvěs (samozřejmě pokud jsou všechna lana stejně dlouhá a nefouká silný vítr).